2017北京石景山高考文科数学一模试卷

标签：高中课外阅读大全,http://www.170xue.com 2017北京石景山高考文科数学一模试卷,http://www.170xue.com
）+cos 2x．

（Ⅰ）求函数f（x）的单调递增区间。

（Ⅱ）在△ABC中，内角A、B、C的对边分别为a、b、c，已知f（A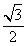）=，a=2，B=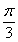，求△ABC的面积．

16．（本小题满分13分）

    PM2．5指大气中直径小于或等于2．5微米的颗粒物，也称为可入肺颗粒物．PM2．5日均值在35微克／立方米以下空气质量为一级：在35微克／立方米～75微克／立方米之间空气质量为二级；在75微克／立方米以上空气质量为超标．

石景山古城地区2013年2月6日至I5日每天的PM2．5监测数据如茎叶图所示．

    （Ⅰ）计算这10天PM2．5数据的平均值并判断其是否超标：

    （Ⅱ）小陈在此期间的某天曾经来此地旅游，求当天PM2．5日均监测数据未超标的概率：

    （III）小王在此期间也有两天经过此地，这两天此地PM2．5监测数据均未超标．请计算出这两天空气质量恰好有一天为一级的概率．

17．（本小题满分14分） 
    如图，在底面为直角梯形的四棱锥P－ABCD中，AD∥BC，∠ABC=90o，PD⊥平面ABCD，AD =1，AB=，BC =4。

    （I）求证：BD⊥PC；

    （II）设AC与BD相交于点D，在棱PC上是否存在点E，使得OE∥平面PAB? 若存在，确定点E位置。

www.170xue.com

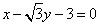
18．（本小题满分14分）

              已知函数f（x）=ax－1－1n x，a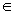R．

    （I）讨论函数f（x）的单调区间：

    （II）若函数f（x）在x=l处取得极值，对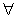x∈（0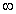，+），f（x）≥bx－2恒成立，求实数b的取值范围．

19．（本小题满分13分）

                设椭圆C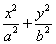：=1（a>b>0）的左、右焦点分别为F1、F2，离心率为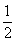，左焦点F1到直线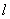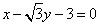：的距离等于长半轴长．

                （I）求椭圆C的方程；

              （II）过右焦点F2作斜率为k的直线l与椭圆C交于M、N两点，线段MN的中垂线与x轴相交于点P（m，O），求实数m的取值范围。

20．（本小题满分13分）

    给定有限单调递增数列{xn}（n∈N*，n≥2）且xi≠0（1≤ i ≤n），定义集合A={（xi，xj）|1≤i，j≤n，且i，j∈N*}．若对任意点A1∈A，存在点A2∈A使得OA1⊥OA2（O为坐标原点），则称数列{xn}具有性质P。

（I）判断数列{xn}：-2，2和数列{yn}：-2，-l，1，3是否具有性质P，简述理由。

（II）若数列{xn}具有性质P，求证：

 ①数列{xn}中一定存在两项xi，xj使得xi+xj =0：

②若x1=-1，  xn>0且xn>1，则x2=l。

上一页  [1] [2] [3] 

，2017北京石景山高考文科数学一模试卷