12-20 22:52:45 浏览次数:216次 栏目：高二数学试题
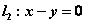截得弦长为
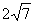的圆的方程．
19．（本大题12分）如图，在棱长为ɑ的正方体ABCD-A1B1C1D1中，E、F、G分别是CB、CD、CC1的中点．
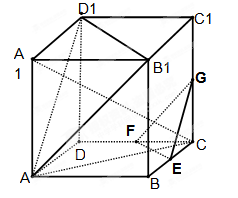
（1）求直线
C与平面ABCD所成角的正弦的值；
（2）求证：平面A B1D1∥平面EFG；
（3
）求证：平面AA1C⊥面EFG ．
第二部分：加试题
（说明：月考成绩为第一部分得分除
以2再加上第二部分得分）
一、填空题：（本题共4小题，每小题5分，共20分，请把答案填写在答题纸上）
1．正四棱锥的侧棱长与底面边长都是2，则侧棱与底面所成角的大小为 .
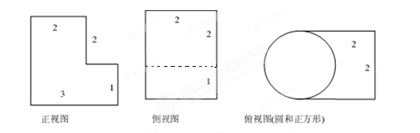
2.下图是一个几何体三视图，根据图中数据，计算该几何体的体积 .
3.已知ABCD是矩形，边长AB=3，BC=4，正方形ACEF边长为5，平面ACEF⊥平面ABCD，则多面体ABCDEF的外接球的表面积 .
4．过点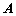
（11，2）作圆
的弦，其中弦长为整数的共有 条.
二、解答题：（本题共2小题，每题15分，共30分，解答应写出文字说明，证明过程或演算步骤.）
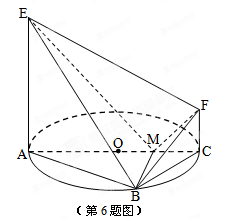
6.(本题15分)如图，AC 是圆 O 的直径，点 B 在圆 O 上，∠BAC＝30°，BM⊥AC交 AC 于点 M，EA⊥平面ABC，FC//EA，AC＝4，EA＝3，FC＝1．
（I）证明：EM⊥BF；
（II）求平面 BEF 与平面ABC 所成锐二面角的余弦值．
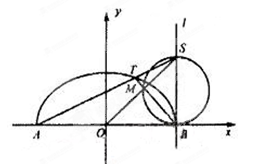
7.（本题15分)已知A，B 分别为曲线C：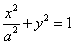
（y≥0，a＞0）与x轴的左、右两个交点，直线
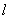过点B，且与x轴垂直，S为
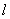上异于点B的一点，连接AS交曲线C于点T．
（1）若曲线C为半圆，点T为圆弧的三等分点，试求出点S的坐
标；
（II）如图，点M是以SB为直径的圆与线段TB的交点，试问：是否存在a，使得O，M，S三点共线？若存在，求出a的值，若不存在，请说明理由．
答案：
必修二模块考部分
18．解：由已知设圆心为（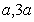
）-
-------1分
与
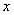轴相切则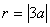
---------2分
圆心到直线的距离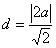
----------3分
弦长为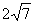
得：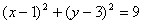
-------6分
解得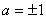
---------7分
圆心为（1，3）或（-1，-3），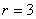
tag: 中学 西湖 考试卷 理科数学 高二数学试题，高二数学试题大全,高二学习方法，高中学习 - 高二学习 - 高二数学 - 高二数学试题
相关分类
高二数学试题 推荐
