12-20 22:52:45 浏览次数:867次 栏目:高考备考
(Ⅱ)设“三人中只有甲破译出密码”为事件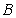 ,则有
,则有
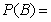
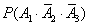 =
=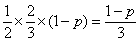 , …………………5分
, …………………5分
所以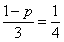 ,
,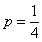 . ……………………7分
. ……………………7分
(Ⅲ)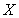 的所有可能取值为
的所有可能取值为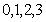 . ……………………8分
. ……………………8分
所以 ,
,
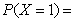
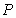
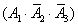
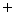
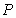
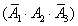
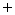
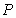
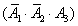
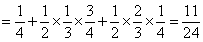 ,
,
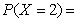
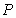
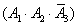
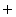
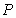
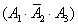
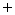
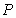
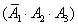
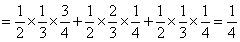 ,
,
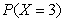 =
=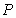
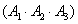 =
=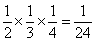 . ……………………11分
. ……………………11分
 分布列为:
分布列为:
编辑推荐:
查看更多有关高考数学的内容,请点击>>高考数学知识点专题
|
x
|
0
|
1
|
2
|
3
|
|
p
|
1/4
|
11/24
|
1/4
|
1/24
|
所以,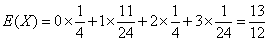 . ………………13分
. ………………13分
编辑推荐:
查看更多有关高考数学的内容,请点击>>高考数学知识点专题
18.(本小题共13分)
(Ⅰ)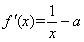 …………………1分
…………………1分
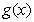 ,
,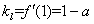 ,所以切线
,所以切线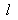 的方程为
的方程为
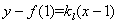 ,即
,即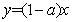 . …………………3分
. …………………3分
(Ⅱ)令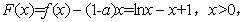 则
则
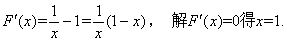 …………………6分
…………………6分
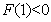 ,所以
,所以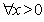 且
且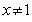 ,
,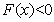 ,
,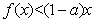 ,
,
即函数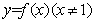 的图像在直线
的图像在直线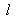 的下方. …………………8分
的下方. …………………8分
(Ⅲ)令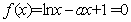 ,
,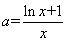 .
.
令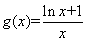 ,
,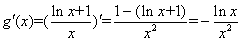 ,
,
则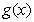 在
在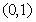 上单调递增,在
上单调递增,在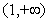 上单调递减,
上单调递减,
当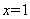 时,
时,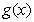 的最大值为
的最大值为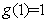 .X|k |B| 1 . c|O |m
.X|k |B| 1 . c|O |m
所以若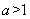 ,则
,则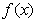 无零点;若
无零点;若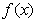 有零点,则
有零点,则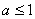 .………………10分
.………………10分
若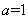 ,
,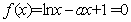 ,由(Ⅰ)知
,由(Ⅰ)知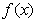 有且仅有一个零点
有且仅有一个零点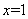 .
.
若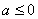 ,
,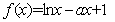 单调递增,由幂函数与对数函数单调性比较,知
单调递增,由幂函数与对数函数单调性比较,知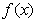 有且仅有一个零点(或:直线
有且仅有一个零点(或:直线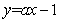 与曲线
与曲线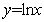 有一个交点).
有一个交点).
若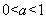 ,解
,解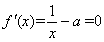 得
得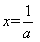 ,由函数的单调性得知
,由函数的单调性得知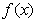 在
在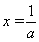 处取最大值,
处取最大值,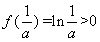 ,由幂函数与对数函数单调性比较知,当
,由幂函数与对数函数单调性比较知,当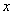 充分大时
充分大时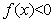 ,即
,即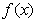 在单调递减区间
在单调递减区间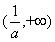 有且仅有一个零点;又因为
有且仅有一个零点;又因为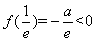 ,所以
,所以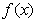 在单调递增区间
在单调递增区间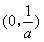 有且仅有一个零点.
有且仅有一个零点.
综上所述,当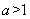 时,
时,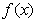 无零点;
无零点;
当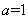 或
或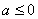 时,
时,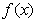 有且仅有一个零点;
有且仅有一个零点;
当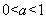 时,
时,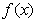 有两个零点. …………………13分
有两个零点. …………………13分
19.(本小题共14分)
(Ⅰ)设椭圆的方程为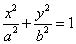 ,因为
,因为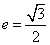 ,所以
,所以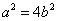 ,
,
又因为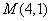 ,所以
,所以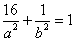 ,解得
,解得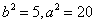 ,
,
故椭圆方程为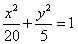 . …………………4分
. …………………4分
(Ⅱ)将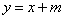 代入
代入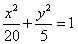 并整理得
并整理得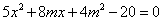 ,
,
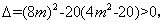 解得
解得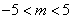 . …………………7分
. …………………7分
(Ⅲ)设直线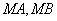 的斜率分别为
的斜率分别为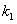 和
和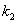 ,只要证明
,只要证明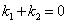 .
.
设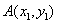 ,
,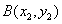 ,
,
则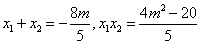 . …………………9分
. …………………9分
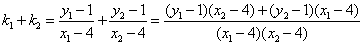
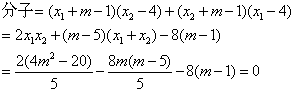
所以直线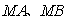 的斜率互为相反数. …………………14分
的斜率互为相反数. …………………14分
20.(本小题共13分)
(Ⅰ)显然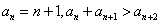 对任意正整数都成立,即
对任意正整数都成立,即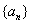 是三角形数列。
是三角形数列。
因为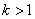 ,显然有
,显然有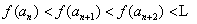 ,
,
由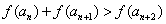 得
得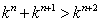
解得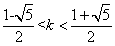 .
.
所以当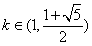 时,
时,
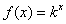 是数列
是数列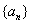 的保三角形函数. …………………3分
的保三角形函数. …………………3分
(Ⅱ)由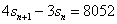 ,得
,得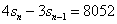 ,
,
两式相减得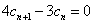 ,所以
,所以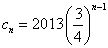 …………………5分
…………………5分
经检验,此通项公式满足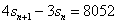 .
.
显然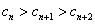 ,
,
因为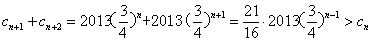 ,
,
所以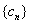 是三角形数列. …………………8分
是三角形数列. …………………8分
(Ⅲ)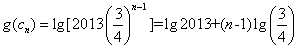 ,
,
所以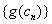 单调递减.
单调递减.
由题意知,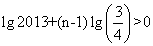 ①且
①且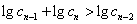 ②,
②,
由①得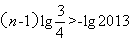 ,解得
,解得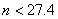 ,
,
由②得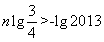 ,解得
,解得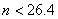 .
.
即数列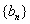 最多有26项. …………………13分
最多有26项. …………………13分
【注:若有其它解法,请酌情给分.】
编辑推荐:
查看更多有关高考数学的内容,请点击>>高考数学知识点专题
,石景山区高三上册数学理科试卷及答案相关分类
高考备考 推荐