初二上册平行线的证明练习题及答案

标签：八年级数学试题,初中数学学习方法,http://www.170xue.com 初二上册平行线的证明练习题及答案,http://www.170xue.com
=9O分，=1OO分．

　　填表对这两种情况分别给予检验（见下表）:　

	语文	数学	外语	常识	奥运	总分	名次
A组	30	4O	4O	4O	3O	18O	1
B组	O	1O	30	3O	40	11O	2
C组	2O	2O	20	O	20	80	3
D组	1O	3O	10	1O	1O	7O	4
E组	4O	O	O	20	O	6O	5

 

	语文	数学	外语	常识	奥运	总分	名次
A组	30	40	4O	4O	30	180	1
B组	1O	1O	1O	3O	40	1OO	2
C组	2O	2O	2O	1O	20	9O	3
D组	0	3O	3O	O	1O	7O	4
E组	40	O	O	20	0	60	5

www.170xue.com

7.3 平行线的判定

　　专题　 平行线的判定的实际应用

　　1．如图，台球运动中，如果母球P击中边点A，经桌边反弹后击中相邻的另一桌边的点B，再次反弹．那么母球P经过的路线BC与PA一定平行．请说明理由．

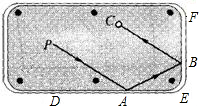
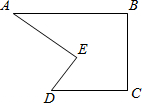
　　2．小明到工厂去进行社会实践活动时，发现工人师傅生产了一种如图所示的零件，要求AB∥CD，∠BAE=35°，∠AED=90°．小明发现工人师傅只是量出∠BAE=35°，∠AED=90°后，又量了∠EDC=55°，于是他就说AB与CD肯定是平行的，你知道什么原因吗？

　　3．如图，某湖上风景区有两个观望点A，C和两个度假村B，D．度假村D在C的正西方向，度假村B在C的南偏东30°方向，度假村B到两个观望点的距离都等于2km．

　　（1）求道路CD与CB的夹角；

　　（2）如果度假村D到C是直公路，长为1km，D到A是环湖路，度假村B到两个观望点的总路程等于度假村D到两个观望点的总路程．求出环湖路的长；

　　（3）根据题目中的条件，能够判定DC∥AB吗？若能，请写出判断过程；若不能，请你加上一个条件，判定DC∥AB．

　　答案：

　　1．解：∵∠PAD=∠BAE，∠PAB=180°-∠PAD-∠BAE，

　　　∴∠PAB=180°-2∠BAE．

　　　同理，∠ABC=180°-2∠ABE．

　　　∵∠BAE+∠ABE=90°，

　　　∴∠PAB+∠ABC=360°-2（∠BAE+∠ABE）=180°．

　　　∴BC∥PA．

　　2．解：AB与CD平行．

　　　理由是：延长AE交DC于M，

　　　∵∠AED=90°，∠EDC=55°，

上一页  [1] [2] [3] [4]  下一页

，初二上册平行线的证明练习题及答案