12-20 22:52:45 浏览次数:672次 栏目:高二数学试题
①若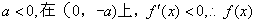 单调递减.
单调递减.
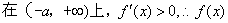 单调递增.
单调递增.
所以, 在
在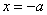 时取得最小值
时取得最小值 ,
,
因为 .
.
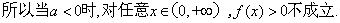 …………………..9分
…………………..9分
② 若 ,
,
所以当 ……………………………………..10分
……………………………………..10分
③若 单调递减.
单调递减.
 单调递增.
单调递增.
所以, 在
在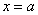 取得最小值
取得最小值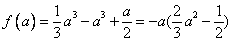 ,
,
令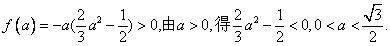

综上, 的取值范围是
的取值范围是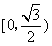 .………………………………13分
.………………………………13分
(19)(本小题满分13分)
解: (Ⅰ)由题意知 ,所以
,所以 .
.
故所求椭圆方程为 ………………………………….5分
………………………………….5分
(Ⅱ) 设直线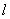 的的方程为
的的方程为 ,则
,则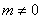 .设
.设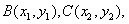
代入椭圆方程并化简得 , …………6分
, …………6分
由 ,可得
,可得 . (
. ( )
)
由( ),得
),得 ,
,
故
tag: 数学 昌平区 高二数学试题,高二数学试题大全,高二学习方法,高中学习 - 高二学习 - 高二数学 - 高二数学试题
相关分类
高二数学试题 推荐