12-20 22:52:45 浏览次数:530次 栏目:高考备考
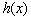 取得最大值
取得最大值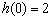 ;
;
(Ⅱ)当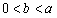 时,
时, .由(1)知:当
.由(1)知:当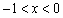 时,
时,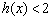 ,即
,即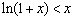 .
.
因此,有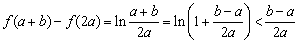 .
.
(Ⅲ)不等式 化为
化为 所以
所以
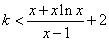 对任意
对任意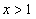 恒成立.令
恒成立.令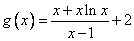 ,则
,则 ,
,
令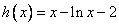
 ,则
,则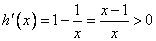 ,所以函数
,所以函数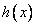 在
在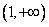 上单调递增.
上单调递增.
因为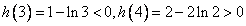 ,
,
所以方程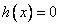 在
在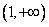 上存在唯一实根
上存在唯一实根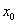 ,且满足
,且满足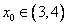 .
.
当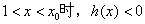 ,即
,即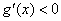 ,当
,当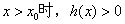 ,即
,即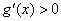 ,
,
所以函数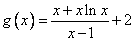 在
在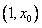 上单调递减,在
上单调递减,在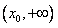 上单调递增.
上单调递增.
所以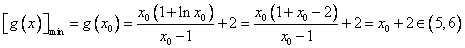 .
.
所以 .故整数
.故整数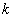 的最大值是
的最大值是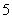 .
.
编辑推荐:
查看更多有关高考数学的内容,请点击>>高考数学知识点专题
,黄埠中学高三上册数学理科试卷及答案相关分类
高考备考 推荐