12-20 22:52:45 浏览次数:274次 栏目:高考数学复习
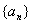 的通项公式,(2)求和还是要先求出数列
的通项公式,(2)求和还是要先求出数列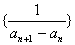 的通项公式,再利用通项公式进行求和。
的通项公式,再利用通项公式进行求和。
解:(1)设等差数列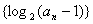 的公差为d,
的公差为d,
由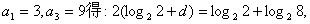 即d=1。
即d=1。
所以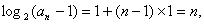 即
即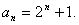
(II)证明:因为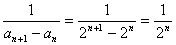 ,
,
所以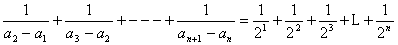
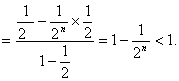
点评:该题通过求通项公式,最终通过通项公式解释复杂的不等问题,属于综合性的题目,解题过程中注意观察规律。
例3.已知数列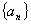 的首项
的首项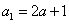 (
(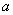 是常数,且
是常数,且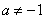 ),
),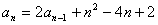 (
(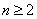 ),数列
),数列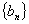 的首项
的首项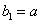 ,
,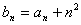 (
(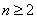 )。
)。
(1)证明: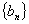 从第2项起是以2为公比的等比数列;
从第2项起是以2为公比的等比数列;
(2)设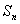 为数列
为数列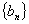 的前n项和,且
的前n项和,且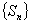 是等比数列,求实数
是等比数列,求实数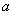 的值。
的值。
分析:第(1)问用定义证明,进一步第(2)问也可以求出。
解:(1)∵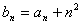 ∴
∴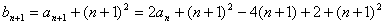
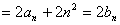 (n≥2)
(n≥2)
由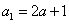 得
得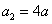 ,
,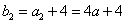 ,∵
,∵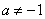 ,∴
,∴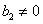 ,
,
即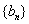 从第2项起是以2为公比的等比数列。
从第2项起是以2为公比的等比数列。
tag: 高考数学 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐