12-20 22:52:45 浏览次数:326次 栏目:高考数学复习
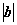 2=0,∴t3-3t-4k=0,即k=
2=0,∴t3-3t-4k=0,即k=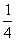 t3-
t3-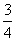 t
t
(2)由(1)知:k=f(t) =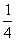 t3-
t3-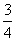 t ∴k´=f´(t) =
t ∴k´=f´(t) =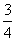 t2-
t2-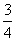 ,
,
令k´<0得-1<t<1;令k´>0得t<-1或t>1.
故k=f(t)的单调递减区间是(-1,1 ),单调递增区间是(-∞,-1)和(1,+∞).
点拨:第1问中两种解法是解决向量垂直的两种常见的方法:一是先利用向量的坐标运算分别求得两个向量的坐标,再利用向量垂直的充要条件;二是直接利用向量的垂直的充要条件,其过程要用到向量的数量积公式及求模公式,达到同样的求解目的(但运算过程大大简化,值得注意)。第2问中求函数的极值运用的是求导的方法,这是新旧知识交汇点处的综合运用。
例2.已知两个力(单位:牛)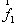 与
与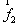 的夹角为
的夹角为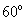 ,其中
,其中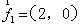 ,某质点在这两个力的共同作用下,由点
,某质点在这两个力的共同作用下,由点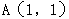 移动到点
移动到点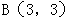 (单位:米)
(单位:米)
(1) 求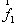 ;
;
(2) 求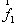 与
与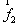 的合力对质点所做的功
的合力对质点所做的功
分析:理解向量及向量数量积的物理意义,将物理中的求力和功的问题转化为向量问题解决.
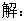
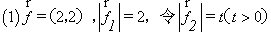
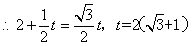
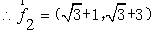
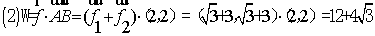
点拨:学习向量要了解向量的实际背景,并能用向量的知识解决方一些简单的实际问题.
【反馈练习】
1.平面直角坐标系中,O为坐标原点,已知两点A(3, 1),B(-1, 3), 若点C满足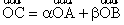 ,其中
,其中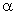 ,
,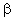 ∈R且
∈R且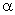 +
+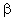 =1,则点C的轨迹方程为x+2y-5=0
=1,则点C的轨迹方程为x+2y-5=0
2.已知a,b是非零向量且满足(a-2b)⊥a,(b-2a)⊥b,则a与b的夹角是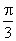
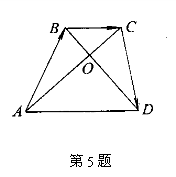
3.已知直线x+y=a与圆x2+y2=4交于A、B两点,且|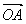 +
+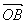
tag: 平面 高考数学 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐