12-20 22:51:02 浏览次数:242次 栏目:初三数学试题
(2)①∵PF=AP=a.∴AF= .OE=OF=
.OE=OF=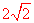 一
一 。
。
∴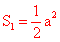 ,
,
∵S1=S2 ,∴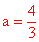 ,解得
,解得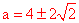 。
。
∵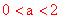 ,∴
,∴ 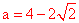 。
。
②不存在。理由如下:
∵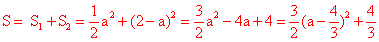 ,
,
∴当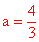 时,S取得最小值为
时,S取得最小值为 。
。
∵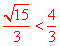 ,∴不存在这样实数a,使S<
,∴不存在这样实数a,使S< 。
。
【考点】圆周角定理,等腰直角三角形的判定和性质,勾股定理,解一元二次方程,二次函数的最值。
【分析】(1)根据已知条件,证出△APF、△OEF与△OAB均为等腰直角三角形即易求出△OEF的面积。
(2)①由S1=S2列出方程,解之即可。
②求出S关于 的函数关系式,由二次函数的最值求出S的最小值,与
的函数关系式,由二次函数的最值求出S的最小值,与 比较即可。
比较即可。
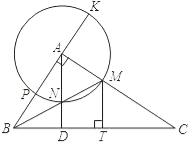
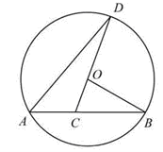
9. (江苏省苏州市2008年9分))如图,在△ABC中,∠BAC=90°,BM平分∠ABC交AC于M,以A
为圆心,AM为半径作OA交BM于N,AN的延长线交BC于D,直线AB交OA于P、K两点.作MT⊥BC
于T
(1)求证AK=MT;
(2)求证:AD⊥BC;
(3)当AK=BD时, 求证: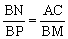 .
.
【答案】证明:(1)∵∠BAC=90°,BM平分∠ABC交AC于M,MT⊥BC,∴AM=MT。
又∵AM=AK,∴AK=MT。
(2)∵BM平分∠ABC交AC于M,∴∠ABM=∠CBM。
又∵AM=AN,∴∠AMN=∠ANM。
又∵∠ANM=∠BND,∴∠AMN=∠BND。
∵∠BAC=900,∴∠ABM+∠AMB=900。∴∠CBM+∠BND=900。
∴∠BDN=900。∴AD⊥BC。
(3)∵BNM和BPK是⊙A的割线,∴BN·BM=BP·BK。即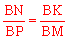 。
。
∵AK=BD,AK=MT,∴BD=MT。
∵AD⊥BC,MT⊥BC,∴∠ADB=∠MTC=900。∴∠C+∠CMT=900。
∵∠BAC=900,∴∠C+∠ABC=900。∴∠ABM=∠CMT。
在△ABD和△CMT中,∵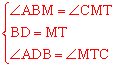 ,∴△ABD≌△CMT(ASA)。
,∴△ABD≌△CMT(ASA)。
∴AB=MC。
∵AK=AM,∴AB+AK=MC+AM,即BK=AC。∴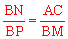 。
。
【考点】角平分线的性质,三角形内角和定理,等腰三角形的性质, 对顶角的性质,垂直的判定,割线长定理,全等三角形的判定和性质。
对顶角的性质,垂直的判定,割线长定理,全等三角形的判定和性质。
【分析】(1)根据角平分线上的点到角两边距离相等的性质,有AM=MT,从而由圆的半径相等结论。
(2)由已知,根据角平分线的性质、等腰三角形的性质和对顶角的性质即能得到∠CBM+∠BND=900的结论,从而根据三角形内角和定理得到∠BDN=900,即AD⊥BC。
(3)根据割线长定理,有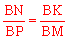 ,故只要证得BK=AC即可证得结论。由△ABD≌△CMT可得AB=MC,由圆半径相等得AK=AM,从而AB+AK=MC+AM,即BK=AC。
,故只要证得BK=AC即可证得结论。由△ABD≌△CMT可得AB=MC,由圆半径相等得AK=AM,从而AB+AK=MC+AM,即BK=AC。
10. (江苏省苏州市2011年8分)如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上的任意一点(不与点A、B重合),连接CO并延长CO交于⊙O于点D,连接AD.
(1)弦长AB等于 ▲ (结果保留根号);
(2)当∠D=20°时,求∠BOD的度数;
(3)当AC的长度为多少时,以A、C、D为顶点的三角形与以B、C、O为顶点的三角形相似?请写出解答过程.
【答案】解: (1)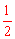
tag: 练习题 初三数学试题,九年级数学试题,初中数学学习方法,初中学习 - 初三学习 - 初三数学 - 初三数学试题
相关分类
初三数学试题 推荐