12-20 22:53:02 浏览次数:656次 栏目:高考备考
若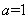 ,
, ,由(Ⅰ)知
,由(Ⅰ)知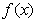 有且仅有一个零点
有且仅有一个零点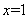 .
.
若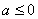 ,
,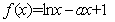 单调递增,由幂函数与对数函数单调性比较,知
单调递增,由幂函数与对数函数单调性比较,知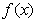 有且仅有一个零点(或:直线
有且仅有一个零点(或:直线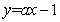 与曲线
与曲线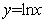 有一个交点).
有一个交点).
若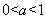 ,解
,解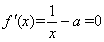 得
得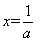 ,由函数的单调性得知
,由函数的单调性得知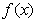 在
在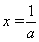 处取最大值,
处取最大值,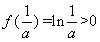 ,由幂函数与对数函数单调性比较知,当
,由幂函数与对数函数单调性比较知,当 充分大时
充分大时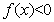 ,即
,即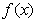 在单调递减区间
在单调递减区间 有且仅有一个零点;又因为
有且仅有一个零点;又因为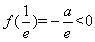 ,所以
,所以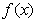 在单调递增区间
在单调递增区间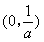 有且仅有一个零点.
有且仅有一个零点.
综上所述,当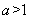 时,
时,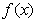 无零点;
无零点;
当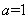 或
或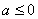 时,
时,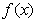 有且仅有一个零点;
有且仅有一个零点;
当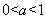 时,
时,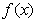 有两个零点. …………………13分
有两个零点. …………………13分
19.(本小题共14分)
(Ⅰ)设椭圆的方程为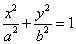 ,因为
,因为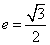 ,所以
,所以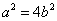 ,
,
又因为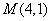 ,所以
,所以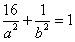 ,解得
,解得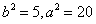
上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] 下一页
,北京石景山区高三上数学期末试题及答案相关分类
高考备考 推荐