12-20 22:52:45 浏览次数:951次 栏目：高考数学复习
解：（1）由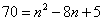
得：
或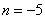
所以70是这个数列中的项，是第13项。
（2）这个数列的前5项是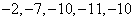
；（图象略）
（3）由函数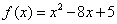
的单调性：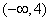
是减区间，
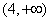是增区间，
所以当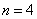
时，
最小，即
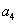最小。
点评：该题考察数列通项的定义，会判断数列项的归属，要注重函数与数列之间的联系，用函数的观点解决数列的问题有时非常方便。
例2．设数列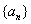
的前n项和为
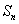，点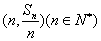
均在函数y＝3x－2的图像上，求数列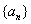的通项公式。
分析：根据题目的条件利用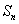与
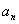的关系：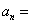
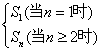，（要特别注意讨论n=1的情况）求出数列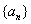的通项。
解：依题意得，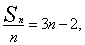
即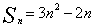
。
当n≥2时，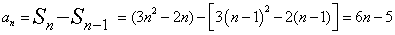
;
当n=1时，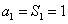
所以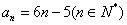
。
例3．已知数列｛a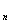
｝满足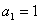
，
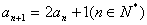
（Ⅰ）求数列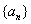的通项公式；
（Ⅱ）若数列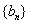
满足
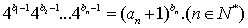，证明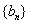：是等差数列;
分析：本题第1问采用构造等比数列来求通项问题，第2问依然是构造问题。
解：（I）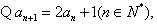
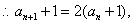
tag: 高考数学 高考数学复习，高考数学复习大全,高考复习方法，高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐
