12-20 22:52:45 浏览次数:419次 栏目:高二数学试题
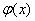 在
在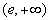 上为减函数,又在x=e处连续,故在
上为减函数,又在x=e处连续,故在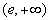 ,
,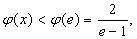 从而要使
从而要使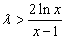 对任意的
对任意的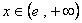 恒成立.只要
恒成立.只要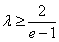 ,故
,故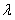 的最小值为
的最小值为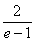 . …………9分
. …………9分
(Ⅲ)一次函数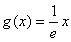 在
在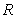 上递增,故函数
上递增,故函数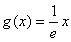 在
在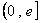 上的值域是
上的值域是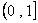 .
.
当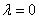 时,
时,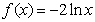 为单调递减函数,不合题意;
为单调递减函数,不合题意;
当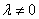 时,
时,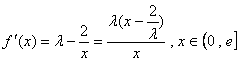 ,要使
,要使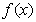 在
在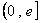 不单调,只要
不单调,只要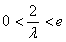 ,此时
,此时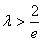 ……①
……①
故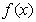 在
在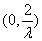 上单调递减,在
上单调递减,在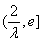 上单调递增.注意到
上单调递增.注意到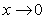 时,
时,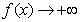
∴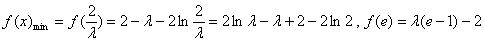
∴对任意给定的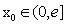 ,在区间
,在区间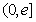 上总存在两个不同的
上总存在两个不同的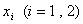 使得
使得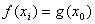 成立,当且仅当
成立,当且仅当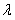 满足下列条件
满足下列条件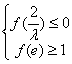
tag: 三明市 数学 高二数学试题,高二数学试题大全,高二学习方法,高中学习 - 高二学习 - 高二数学 - 高二数学试题
相关分类
高二数学试题 推荐