12-20 22:53:02 浏览次数:290次 栏目:高考备考
19.(本题13分)已知以原点为对称中心、F(2,0)为右焦点的椭圆C过点P(2,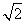 ),直线
),直线 :y=kx+m(k≠0)交椭圆C于不同的两点A、B。
:y=kx+m(k≠0)交椭圆C于不同的两点A、B。
(Ⅰ)求椭圆C的方程;
(Ⅱ)是否存在k的值,使线段AB的垂直平分线经过点Q(0,3),若存在求出 k的取值范围,若不存在,请说明理由。
解:(Ⅰ)设椭圆C的方程为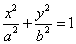
 ,由题意
,由题意
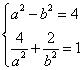 ,解得
,解得 ,
,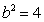 ,所以椭圆C的方程为
,所以椭圆C的方程为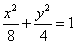 . ……………………5分
. ……………………5分
(Ⅱ)假设存在斜率为k的直线,其垂直平分线经过点Q(0,3),
设A(x1,y1)、B(x2,y2),AB的中点为N(x0,y0),
由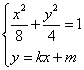 得
得 , ……………………………………………6分
, ……………………………………………6分
 ,所以
,所以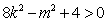 ,……………7分
,……………7分
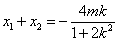 ,
,

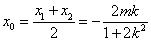 ,
,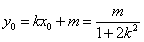 , …………………………………………8分
, …………………………………………8分
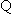 线段AB的垂直平分线过点Q(0,3),
线段AB的垂直平分线过点Q(0,3),

 ,即
,即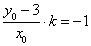 ,
,
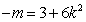 , ………………………………………10分
, ………………………………………10分
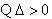 ,整理得
,整理得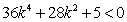 ,显然矛盾
,显然矛盾 不存在满足题意的k的值。……………………………13分
不存在满足题意的k的值。……………………………13分
(Ⅲ)(1)当k=n时,显然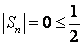 成立;…………………………………………………9分
成立;…………………………………………………9分
当k
 ,
,
即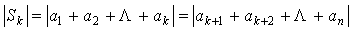 ,
,

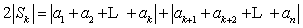
相关分类
高考备考 推荐