12-20 22:52:45 浏览次数:899次 栏目：高考备考
17．在一次抽奖活动中，有甲、乙等6人获得抽奖的机会。抽奖规则如下：主办方先从6人中随机抽取两人均获奖1000元，再从余下的4人中随机抽取1人获奖600元，最后还从这4人中随机抽取1人获奖400元。
（Ⅰ）求甲和乙都不获奖的概率；
（Ⅱ）设X是甲获奖的金额，求X的分布列和均值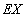
。
18.已知函数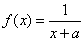
，
.
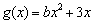(Ⅰ)若曲线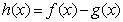
在点（1，0）处的切线斜率为0，求a，b的值；
(Ⅱ)当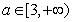
，且ab=8时，求函数
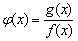的单调区间，并求函数在区间[-2，-1]上的最小值。
19． 已知以原点为对称中心、F(2，0)为右焦点的椭圆C过P(2，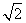
)，直线
：y=kx+m(k≠0)交椭圆C于不同的两点A，B。
（Ⅰ）求椭圆C的方程；
（Ⅱ）是否存在实数k，使线段AB的垂直平分线经过点Q（0，3）？若存在求出 k的取值范围；若不存在，请说明理由。
20． 设满足以下两个条件的有穷数列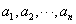
为n（n=2，3，4，…，）阶“期待数列”：
①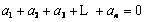
；
②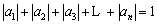
.
（Ⅰ）分别写出一个单调递增的3阶和4阶“期待数列”；
（Ⅱ）若某2k+1(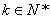
)阶“期待数列”是等差数列，求该数列的通项公式；
（Ⅲ）记n阶“期待数列”的前k项和为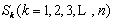
，
试证：（1）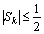
； （2）
相关分类
高考备考 推荐
