12-20 22:52:45 浏览次数:197次 栏目:高考数学复习
∴ 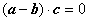
(2)∵ 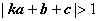 ,即
,即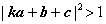
也就是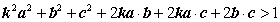
∵ 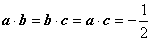 ,∴
,∴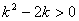
所以 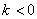 或
或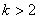 .
.
解:对于有关向量的长度、夹角的求解以及垂直关系的判断通常是运用平面向量的数量积解决.
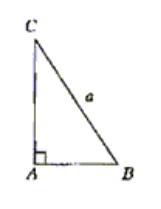
例3.如图,在直角△ABC中,已知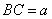 ,若长为
,若长为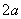 的线段
的线段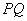 以点
以点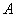 为中点,问
为中点,问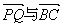 的夹角
的夹角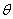 取
取
何值时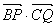 的值最大?并求出这个最大值
的值最大?并求出这个最大值
分析:本题涉及向量较多,可通过向量的加减法则得
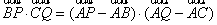 ,再结合直角三
,再结合直角三
角形和各线段长度特征法解决问题
解: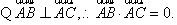
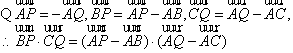


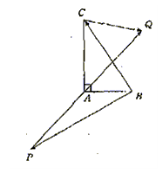
点拨:运用向量的方法解决几何问题,充分体现了向量的工具性,对于大量几何问题,不仅可以用向量语言加以叙述,而且完全可以借助向量的方法予以证明和求解,从而把抽象的问题转化为具体的向量运算.
【反馈练习】
1.已知向量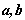 满足
满足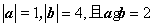
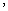 则
则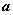 与
与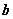 的夹角为
的夹角为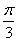
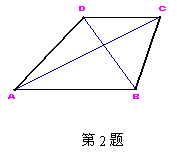
2.如图,在四边形ABCD中,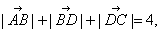
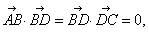
tag: 平面 高考数学 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐