12-20 22:52:45 浏览次数:197次 栏目:高考数学复习
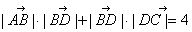 ,则
,则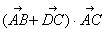 的值为4
的值为4
3.若向量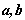 满足
满足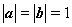 ,
,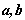 的夹角为60°,则
的夹角为60°,则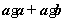 =
=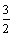
4.若向量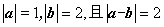 ,则
,则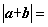
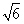
5.已知| a|=4,|b|=5,|a+b|=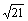 ,求:① a·b ;②(2a-b) ·(a+3b)
,求:① a·b ;②(2a-b) ·(a+3b)
解:(1)|a+b|2=(a+b)2=a2+2ab+b2=|a|2+2a·b+|b|2,∴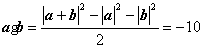
(2)(2a-b)·(a+3b)=2a2+5a·b-3b2=2|a|2+5a·b-3|b|2=2×42+5×(-10)-3×52=-93.
6.已知a与b都是非零向量,且a+3b与7a-5b垂直,a-4b与7a-2b垂直,求a与b的夹角.
解:∵且a+3b与7a-5b垂直,a-4b与7a-2b垂直,
∴(a+3b)·(7a-5b)=0,(a-4b)·(7a-2b)=0 ∴7a2+16a·b-15 b2=0,7a2-30a·b+8 b2=0,
∴b2=2a·b,|a|=|b| ∴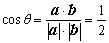 ∴
∴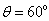
tag: 平面 高考数学 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐