12-20 22:58:55 浏览次数:772次 栏目:高考数学复习
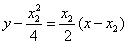 (2)
(2)
解(1)( 2)构成的方程组可得点M的坐标,从而得到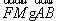 =0 即为定值
=0 即为定值
(2)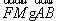 =0可得
=0可得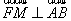 三角形面积
三角形面积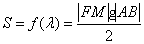

所以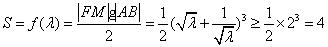
当且仅当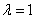 时取等号
时取等号
点拨:本题主要考察共线向量的关系,曲线的切线方程,直线的交点以及向量的数量积等知识点
涉及均值不等式,计算较复杂.难度很大
【反馈练习】
1.已知双曲线的中心在原点,离心率为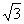 .若它的一条准线与抛物线
.若它的一条准线与抛物线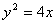 的准线重合,则该双曲线与抛物线
的准线重合,则该双曲线与抛物线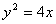 的交点到原点的距离是
的交点到原点的距离是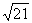
2.设 分别是双曲线
分别是双曲线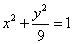 的左、右焦点.若点
的左、右焦点.若点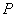 在双曲线上,且
在双曲线上,且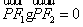 ,则
,则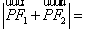
3.设P是椭圆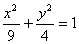 上一点,
上一点,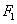 、
、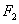 是椭圆的两个焦点,则
是椭圆的两个焦点,则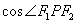 的最小值是
的最小值是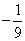
4.已知以F1(2,0),F2(2,0)为焦点的椭圆与直线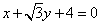 有且仅有一个交点,则椭圆的长轴长为
有且仅有一个交点,则椭圆的长轴长为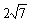
5. 双曲线C与椭圆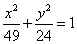 的焦点相同,离心率互为倒数,则双曲线C的渐近线的方程是
的焦点相同,离心率互为倒数,则双曲线C的渐近线的方程是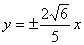
6.已知椭圆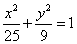 与双曲线
与双曲线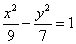 在第一象限内的交点为
在第一象限内的交点为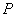 ,则点
,则点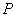 到椭圆右焦点的距离等于__2 _
到椭圆右焦点的距离等于__2 _
7.如图,点A是椭圆C: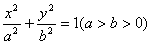
tag: 圆锥曲线 高考数学 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐