初三上册数学期末试卷及答案（人教版）

标签：中考试题大全,中考复习计划,http://www.170xue.com 初三上册数学期末试卷及答案（人教版）,http://www.170xue.com

　　当两张硬纸片上的图形可拼成电灯或小人时，杨华得1分；

　　当两张硬纸片上的图形可拼成房子或小山时，季红得1分（如图2）．

　　问题：游戏规则对双方公平吗？请说明理由；若你认为不公平，如何修改游戏规则才能使游戏对双方公平？

　　20．（9分）如图，已知直线y=﹣x+4与反比例函数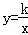的图象相交于点A（﹣2，a），并且与x轴相交于点B．

　　（1）求a的值；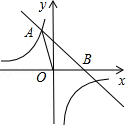

　　（2）求反比例函数的表达式；

　　（3）求△AOB的面积．

　

　　五、（21、22题各10分）

　　21．（10分）将一块正方形铁皮的四个角各剪去一个边长为4cm的小正方形，做成一个无盖的盒子，盒子的容积是400cm3，求原铁皮的边长．

　　22．（10分）（2010•安顺）已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，

　　（1）求证：四边形ADCE为矩形；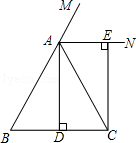

　　（2）当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明．

　

　

　　六、（23、24题各10分）

　　23．（10分）某花圃用花盆培育某种花苗，经过实验发现每盆的盈利与每盆的株数构成一定的关系．每盆植入3株时，平均单株盈利3元；以同样的栽培条件，若每盆增加1株，平均单株盈利就减少0.5元．要使每盆的盈利达到10元，每盆应该植多少株？

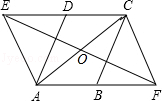
　　24．（10分）（2006•中山）如图，在?ABCD中，∠DAB=60°，点E、F分别在CD、AB的延长线上，且AE=AD，CF=CB．

　　（1）求证：四边形AFCE是平行四边形；

　　（2）若去掉已知条件的“∠DAB=60°”，上述的结论还成立吗？若成立，请写出证明过程；若不成立，请说明理由．

　　七、（12分）

　　25．（12分）已知反比例函数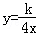和一次函数y=2x﹣1，其中一次函数的图象经过（a，b），（a+2，b+k）两点．

　　（1）求：反比例函数的解析式．

　　（2）如图，已知点A在第一象限，且同时在上述两函数的图象上．求点A的坐标．

　　（3）利用（2）的结果，问在x轴上是否存在点P，使得△AOP为等腰三角形？若存在，把符合条件的P点坐标直接写出来；若不存在，说明理由．

　　八、（14分）

　　26．（14分）（2010•鞍山）在等腰梯形ABCD中，AB=DC=5，AD=4，BC=10．点E在下底边BC上，点F在腰AB上．

　　（1）若EF平分等腰梯形ABCD的周长，设BE长为x，试用含x的代数式表示△BEF的面积；

　　（2）是否存在线段EF将等腰梯形ABCD的周长和面积同时平分？若存在，求出此时BE的长；若不存在，请说明理由；

　　（3）是否存在线段EF将等腰梯形ABCD的周长和面积同时分成1：2的两部分？若存在，求出此时BE的长；若不存在，请说明理由．

 

　　参考答案：　　

　　一、精心选一选（本大题共8小题，每小题3分，共24分）

　　1．考点：平行投影．

　　分析：解：根据平行投影的特点和规律可知，C，D是上午，A，B是下午，根据影子的长度可知先后为C→D→A→B．

　　解答：解：根据平行投影的特点和规律可知，C，D是上午，A，B是下午，

　　根据影子的长度可知先后为C→D→A→B．

　　故选C．

　　点评：本题考查平行投影的特点和规律．在不同时刻，同一物体的影子的方向和大小可能不同，不同时刻物体在太阳光下的影子的大小在变，方向也在改变，就北半球而言，从早晨到傍晚物体的指向是：西﹣西北﹣北﹣东北﹣东，影长由长变短，再变长．

　　2．考点：勾股定理；解一元二次方程-因式分解法．

　　专题：分类讨论．

　　分析：求出方程的解，得出直角三角形的两边长，分为两种情况：①当3和4是两直角边时，②当4是斜边，3是直角边时，根据勾股定理求出第三边即可．

　　解答：解：x²﹣7x+12=0，

　　（x﹣3）（x﹣4）=0，

　　x﹣3=0，x﹣4=0，

　　解得：x₁=3，x₂=4，

　　即直角三角形的两边是3和4，

　　当3和4是两直角边时，第三边是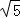=5；

　　当4是斜边，3是直角边时，第三边是 =，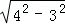

　　即第三边是5或，

　　故选D．

　　点评：本题考查了解一元二次方程和勾股定理，注意：解此题时要进行分类讨论．

　　3．考点：一元二次方程的解．

　　专题：计算题．

　　分析：一元二次方程的根就是一元二次方程的解，就是能够使方程左右两边相等的未知数的值；即用这个数代替未知数所得式子仍然成立；将x=3代入原方程即可求得2a的值．

　　解答：解：把x=3代入原方程得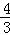：×9﹣2a+1=0，

　　∴2a=13；

　　故选C．

　　点评：本题考查的是一元二次方程的根即方程的解的定义．

　　4．考点：命题与定理．

　　分析：利用梯形可对A进行判断；根据平行四边形的判定方法对B进行判断；根据等腰梯形的性质对C进行判断；根据平行四边形的性质对D进行判断．

　　解答：解：A、直角梯形的一对邻角互补，所以A选项的命题为假命题；

　　B、一组对边平行，一组对角相等的四边形是平行四边形，所以B选项为真命题；

　　C、等腰梯形的对角线相等，所以C选项为真命题；

　　D、平行四边形的对角线互相平分，所以D选项为真命题．

　　故选A．

　　点评：本题考查了命题与定理：判断事物的语句叫命题；正确的命题称为真命题，错误的命题称为假命题；经过推理论证的真命题称为定理．

上一页  [1] [2] [3] [4] [5] [6] [7] [8]  下一页

，初三上册数学期末试卷及答案（人教版）