12-20 22:59:14 浏览次数:370次 栏目:中考试题
点评:此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=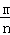 .
.
11.18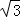 考点:菱形的性质.
考点:菱形的性质.
分析:根据菱形对角线垂直且互相平分,且每条对角线平分它们的夹角,即可得出菱形的另一一条对角线长,再利用菱形的面积公式求出即可.
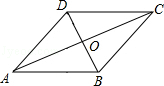
解答:解:如图所示:∵菱形有一个内角为60°,较短的对角线长为6,
∴设∠BAD=60°,BD=6,
∵四边形ABCD是菱形,
∴∠BAC=∠DAC=30°,DO=BO=3,
∴AO=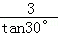 =3
=3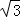 ,
,
∴AC=6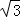 ,则它的面积为:
,则它的面积为: ×6×6
×6×6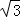 =18
=18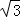 .
.
故答案为:18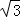 .
.
点评:此题主要考查了菱形的性质,熟练掌握菱形的面积公式以及对角线之间的关系是解题关键.
12.矩形考点:矩形的判定;平行线的性质;三角形中位线定理;平行四边形的判定;菱形的性质.
专题:证明题.
分析:连接AC、BD交于O,根据三角形的中位线定理推出EF∥BD∥HG,EH∥AC∥FG,得出四边形EFGH是平行四边形,根据菱形性质推出AC⊥BD,推出EF⊥EH,即可得出答案.
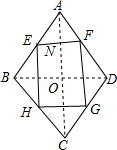 解答:解:连接AC、BD交于O,
解答:解:连接AC、BD交于O,
∵E、F、G、H分别是AB、AD、CD、BC的中点,
∴EF∥BD,FG∥AC,HG∥BD,EH∥AC,
∴EF∥HG,EH∥FG,
∴四边形EFGH是平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,
∵EF∥BD,EH∥AC,
∴EF⊥EH,
∴∠FEH=90°,
∴平行四边形EFGH是矩形,
故答案为:矩形.
点评:本题考查了矩形的判定,菱形的性质,平行四边形的判定,平行线性质等知识点的运用,主要考查学生能否正确运用性质进行推理,题目比较典型,难度适中.
13.空心的圆柱考点:由三视图判断几何体.
分析:两个视图是矩形,一个视图是个圆环,那么符合这样条件的几何体是空心圆柱.
解答:解:如图,该几何体的三视图中两个视图是矩形,一个视图是个圆环,故该几何体为空心圆柱.
点评:本题考查由三视图确定几何体的形状,主要考查学生空间想象能力及对立体图形的认知能力.
14.(x+2)2﹣100 .考点:配方法的应用.
专题:计算题.
分析:前两项加上4再减去4变形,利用完全平方公式化简即可得到结果.
解答:解:x2+4x﹣96=x2+4x+4﹣100=(x+2)2﹣100.
故答案为:(x+2)2﹣100
点评:此题考查了配方法的应用,熟练掌握完全平方公式是解本题的关键.
15.30考点:平行四边形的性质.
专题:计算题;压轴题.
分析:要使其面积为矩形面积的一半,平行四边形ABCD的高必须是矩形宽的一半,根据直角三角形中30°的角对的直角边等于斜边的一半可知,这个平行四边形的最小内角等于30度.
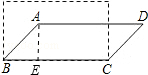
解答:解:∵平行四边形的面积为矩形的一半且同底BC,
∴平行四边形ABCD的高AE是矩形宽AB的一半.
在直角三角形ABE中,AE=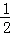 AB,
AB,
∴∠ADC=30°.
故答案为30.
点评:主要考查了平行四边形的面积公式和基本性质.平行四边形的面积等于底乘高.
16.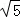 考点:正方形的性质;全等三角形的判定与性质;勾股定理.
考点:正方形的性质;全等三角形的判定与性质;勾股定理.
分析:标注字母,根据正方形的性质可得AB=AD,∠BAD=90°,再根据同角的余角相等求出∠1=∠3,然后利用“角角边”字母△ABE和△DAF全等,根据全等三角形对应边相等可得AE=DF,再利用勾股定理列式计算即可得解.
解答:解:如图,由正方形可得,AB=AD,∠BAD=90°,
∠1+∠2=180°﹣90°=90°,
∵BE⊥AE,∴∠2+∠3=180°﹣90°=90°,
∴∠1=∠3,
在△ABE和△DAF中,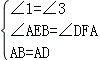 ,
,
∴△ABE≌△DAF(AAS),
∴AE=DF=1,
在Rt△ABE中,AB=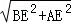 =
=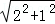 =
=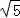 ,
,
即正方形的边长为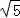
tag: 数学 中考试题,中考试题大全,中考复习计划,初中学习 - 初三学习 - 中考试题
相关分类
中考试题 推荐