初三上册数学期末试卷及答案（人教版）

标签：中考试题大全,中考复习计划,http://www.170xue.com 初三上册数学期末试卷及答案（人教版）,http://www.170xue.com
OB×AD=×4×6=12．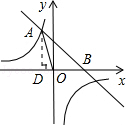

点评：熟练掌握解析式的求法．在进行与线段有关的计算时，注意点的坐标与线段长度的关系．

 

 

　　五、（21、22题各10分）

　　21．考点：一元二次方程的应用．

　　专题：几何图形问题．

　　分析：本题可设原铁皮的边长为xcm，将这块正方形铁皮四个角各剪去一个边长为4cm的小正方形，做成一个无盖的盒子后，盒子的底面积变为（x﹣2×4）²，其高则为4cm，根据体积公式可列出方程，然后解方程求出答案即可．

　　解答：解：设原铁皮的边长为xcm，

　　依题意列方程得（x﹣2×4）²×4=400，

　　即（x﹣8）²=100，

　　所以x﹣8=±10，

　　x=8±10．

　　所以x₁=18，x₂=﹣2（舍去）．

　　答：原铁皮的边长为18cm．

　　点评：这类题目体现了数形结合的思想，通常把实际问题转换为方程求解，但应注意考虑解得合理性，即考虑解的取舍．

　　22．考点：矩形的判定；角平分线的性质；等腰三角形的性质；正方形的判定．

　　专题：证明题；开放型．

　　分析：（1）根据矩形的有三个角是直角的四边形是矩形，已知CE⊥AN，AD⊥BC，所以求证∠DAE=90°，我样可以证明四边形ADCE为矩形．（2）根据正方形的判定，我们可以假设当AD=BC，由已知可得，DC=BC，由（1）的结论可知四边形ADCE为矩形，所以证得，四边形ADCE为正方形．

　　解答：（1）证明：在△ABC中，AB=AC，AD⊥BC，

　　∴∠BAD=∠DAC，

　　∵AN是△ABC外角∠CAM的平分线，

　　∴∠MAE=∠CAE，

　　∴∠DAE=∠DAC+∠CAE=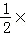180°=90°，

　　又∵AD⊥BC，CE⊥AN，

　　∴∠ADC=∠CEA=90°，

　　∴四边形ADCE为矩形．

　　（2）当△ABC满足∠BAC=90°时，四边形ADCE是一个正方形．

　　理由：∵AB=AC，

　　　　　∴∠ACB=∠B=45°，

　　　　　∵AD⊥BC，

　　　　　∴∠CAD=∠ACD=45°，

　　　　　∴DC=AD，

　　　　　∵四边形ADCE为矩形，　

　　　　　∴矩形ADCE是正方形．

　　　　　∴当∠BAC=90°时，四边形ADCE是一个正方形．

　　点评：本题是以开放型试题，主要考查了对矩形的判定，正方形的判定，等腰三角形的性质，及角平分线的性质等知识点的综合运用．

　　六、（23、24题各10分）

　　23．考点：一元二次方程的应用．

　　分析：根据已知假设每盆花苗增加x株，则每盆花苗有（x+3）株，得出平均单株盈利为（3﹣0.5x）元，由题意得（x+3）（3﹣0.5x）=10求出即可．

　　解答：解：设每盆花苗增加x株，则每盆花苗有（x+3）株，

　　平均单株盈利为：（3﹣0.5x）元，

　　由题意得：（x+3）（3﹣0.5x）=10．

　　化简，整理，的x²﹣3x+2=0．

　　解这个方程，得x₁=1，x₂=2，

　　则3+1=4，2+3=5，

　　答：每盆应植4株或者5株．

　　点评：此题考查了一元二次方程的应用，根据每盆花苗株数×平均单株盈利=总盈利得出方程是解题关键．

　　24．考点：平行四边形的判定与性质；全等三角形的判定与性质．

　　专题：证明题；探究型．

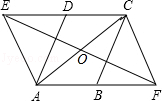
　　分析：（1）由已知条件可得△AED，△CFB是正三角形，可得∠AEC=∠BFC=60°，∠EAF=∠FCE=120°，所以四边形AFCE是平行四边形．

　　（2）上述结论还成立，可以证明△ADE≌△CBF，可得∠AEC=∠BFC，∠EAF=∠FCE，所以四边形AFCE是平行四边形．

　　解答：（1）证明：∵四边形ABCD是平行四边形，

　　　　　∴DC∥AB，∠DCB=∠DAB=60°．

　　　　　∴∠ADE=∠CBF=60°．

　　　　　∵AE=AD，CF=CB，

　　　　　∴△AED，△CFB是正三角形．

　　　　　∴∠AEC=∠BFC=60°，∠EAF=∠FCE=120°．

　　　　　∴四边形AFCE是平行四边形．

　　（2）解：上述结论还成立．

　　证明：∵四边形ABCD是平行四边形，

　　　　　∴DC∥AB，∠CDA=∠CBA，∠DCB=∠DAB，AD=BC，DC=AB．

　　　　　∴∠ADE=∠CBF．

　　　　　∵AE=AD，CF=CB，

　　　　　∴∠AED=∠ADE，∠CFB=∠CBF．

　　　　　∴∠AED=∠CFB．

　　　　　又∵AD=BC，在△ADE和△CBF中．，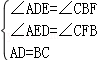

　　　　　∴△ADE≌△CBF（AAS）．

　　　　　∴∠AED=∠BFC，∠EAD=∠FCB．

　　　　　又∵∠DAB=∠BCD，∴∠EAF=∠FCE．

　　　　　∴四边形EAFC是平行四边形．

　　点评：本题考查了等边三角形的性质及平行四边形的判定．多种知识综合运用是解题中经常要遇到的．

　　七、（12分）

　　25．考点：反比例函数综合题．

　　分析：（1）先把（a，b）、（a+2，b+k）代入y=2x+1得到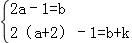，然后结果代数式变形可解得k=4，则可确定反比例函数解析式；

　　（2）把一次函数与反比例函数解析式组成方程组，再解方程组可确定A点坐标；

　　（3）先利用勾股计算出OA=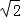，过A点作AP₁⊥x轴，则△OAP₁为等腰三角形；作点O关于AP₁的对称点P₂，则△OAP₂为等腰三角形；以O点为圆心，OA为半径画弧交x轴与P₃，P₄，则△OAP₃、△OAP₄为等腰三角形；然后利用线段长分别确定各点坐标．

　　解答：解：（1）把（a，b）、（a+2，b+k）代入y=2x+1得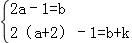，解得k=4，

　　所以反比例函数解析式为y=

上一页  [1] [2] [3] [4] [5] [6] [7] [8]  下一页

，初三上册数学期末试卷及答案（人教版）