12-20 22:59:14 浏览次数:370次 栏目:中考试题
(2)解方程组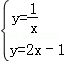 得
得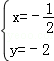 或
或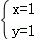 ,
,
∵A点在第一象限,
∴点A的坐标为(1,1);
(3)存在.
OA=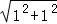 =
=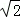 ,
,
满足条件的点P坐标为( 1,0)、(2,0)、(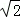 ,0)、(﹣
,0)、(﹣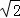 ,0).
,0).
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、等腰三角形的判定与性质;运用分类讨论的思想解决问题.
八、(14分)
26.考点:等腰梯形的性质;一元二次方程的应用.
专题:压轴题;开放型.
分析:(1)先作AK⊥BC于K,FG⊥BC于G,根据等腰梯形的性质,可得BK=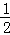 (BC﹣AD)=3,在Rt△ABK中,利用勾股定理可求出AK=4,由于AK、FG垂直于同一直线故平行,可得比例线段,求出FG=
(BC﹣AD)=3,在Rt△ABK中,利用勾股定理可求出AK=4,由于AK、FG垂直于同一直线故平行,可得比例线段,求出FG=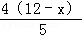 ,利用面积公式可得S△BEF=﹣
,利用面积公式可得S△BEF=﹣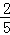 x2+
x2+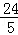 x(7≤x≤10,因为BF最大取5,故BE最小取7,又不能超过10);(2)根据题意,结合(1)中面积的表达式,可以得到
x(7≤x≤10,因为BF最大取5,故BE最小取7,又不能超过10);(2)根据题意,结合(1)中面积的表达式,可以得到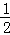 S梯形ABCD=﹣
S梯形ABCD=﹣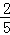 x2+
x2+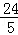 x,即14=﹣
x,即14=﹣ x2+
x2+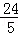 x,解得,x1=7,x2=5(不合题意,舍去);
x,解得,x1=7,x2=5(不合题意,舍去);
(3)仍然按照(1)和(2)的步骤和方法去做就可以了,注意不是分成相等的两份,而是1:2就可以了,得到关于x的一元二次方程,先求出根的判别式△,由于△<0,故不存在实数根.
解答:解:(1)由已知条件得:
梯形周长为24,高4,面积为28.
过点F作FG⊥BC于G
∴BK= (BC﹣AD)=
(BC﹣AD)= ×(10﹣4)=3,
×(10﹣4)=3,
∴AK=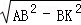 =4,
=4,
∵EF平分等腰梯形ABCD的周长,设BE长为x,
∴BF=12﹣x,
过点A作AK⊥BC于K
∴△BFG∽△BAK,
∴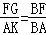 ,
,
即: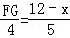 ,
,
则可得:FG=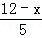 ×4
×4
∴S△BEF=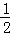 BE•FG=﹣
BE•FG=﹣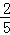 x2+
x2+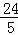 x(7≤x≤10);(3分)
x(7≤x≤10);(3分)
(2)存在(1分)
由(1)得:﹣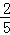 x2+
x2+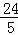 x=14,
x=14,
x2﹣12x+35=0,
(x﹣7)(x﹣5)=0,
,初三上册数学期末试卷及答案(人教版)tag: 数学 中考试题,中考试题大全,中考复习计划,初中学习 - 初三学习 - 中考试题
相关分类
中考试题 推荐